こんな人に読んでもらいたい記事です
・資産形成を始めてみたけど「72の法則」って何?
・「70の法則」や「74の法則」じゃだめなん?
・指数関数がどんなところで役立つのか見てみたい
という人
結論
・資産形成で有名な「72の法則」ですが,
指数関数,対数関数で噛み砕いてみました.
・「72の法則」はあくまで
だいたいの目安を示しているにすぎない
・インデックスファンドでの長期投資を
考えたらある程度合理的な法則.
・正確な年数を知りたいなら,
対数関数を計算してみよう.![]()
「72の法則」を勝手に疑ってみました
こんにちはりゅういえんじにあです.
突然ですが資産形成をはじめました.
資産形成をするにあたって,
いろいろ調べてみると「72の法則」なる
ものがあることがわかりました.
「この72の法則ってほんとかよ!」と思ったので,
りゅういえんじにあが数学的な計算をして
確認してみました.
どういう計算かというと,
「指数関数」「対数関数」です.
これは高校数学の範囲です.
資産形成の世界でも,
高校数学の知識は役に立つんだよ,
ということをお伝えできればと思います.
資産形成を始めるにあたって以下の書籍が参考になります.
そもそも「72の法則」ってなんぞや?
「72の法則」は資産運用の世界では
割とメジャーな法則で,
元本が2倍にかかるまでにかかる年数は
およそ72/X年」です.
と計算できる,というものです.
「72の法則」は、資産を倍にするために必要な年数を計算するために、72を予定運用利回りで割るだけである。それだけで資産を倍にするために必要な年数がでてくる。
指数関数・対数関数の知識で追っかけてみる
72という数字は様々な数で割り切ることができるため,
比較的計算しやすく,使い勝手が良いという側面があります.
ただ今回の趣旨はこの「72の法則」を
「使い勝手がよい」で終わらせるのではなく,
数学的に追っかけていこうというものです.
年利X%でn年運用したらもとの資産(元本)はどうなる?
最初の資産(元本)を1としたとき,
1年後の資産は
(1+0.01x)です.
また1年経過すると
(1+0.01x)(1+0.01x)です.
このように
1年経過するごとに(1+0.01x)を
掛け算していくことで,年利で増えたお金を
計算できます.
このように
元本1で年利X%でn年運用したら
もとの資産(元本)は
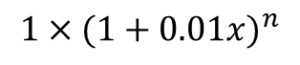
のように表されます.(式.1)
「72の法則」を求めてみよう
結論:72という数字はダイレクトに決まるものではない
さて,72の法則は元本が2倍になるのは何年後?
ということを求めるものです.
では先程の式の結果が2(元本1の2倍)に
なれば良いので,式は以下のようになります.
(式.2)
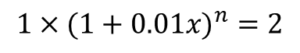
式をうまく捏ねくり回し,
Xとnの関係をうまく求めて
n=72/X
になることを確認するのが目的です.
が,実は対数の定義に従って
式.2を捏ねくり回しても
72という数字は出てきません.
それもそのはず,72という数字は
「だいたいこれくらいじゃね?」という
目安にしかすぎないからです.
「70の法則」や「74の法則」じゃだめなのか?
72が目安にすぎない,ということは
「70の法則」や「74の法則」じゃダメなのか,
と思い実際に計算してみました.
以下がその結果です.
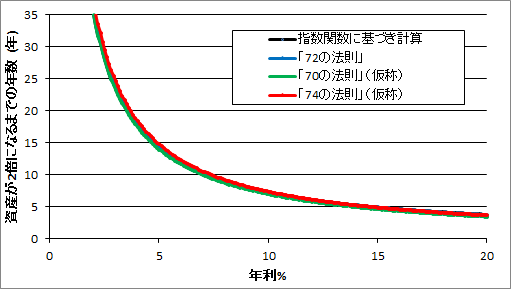
意外と厳密に計算した場合と比べても
「72の法則」や「70の法則」,「74の法則」
で計算した結果が重なっているように見えます.
うーむ,思ったより
「70の法則」や「74の法則」でも
良い気がするぞ,というのが正直な感想です.
そこで「72」という数字を
もう少し詳しく検証するために,
厳密に計算した場合の年数と
それぞれの法則で計算した場合に
資産が2倍になる年数の差(誤差)を
計算してみました.
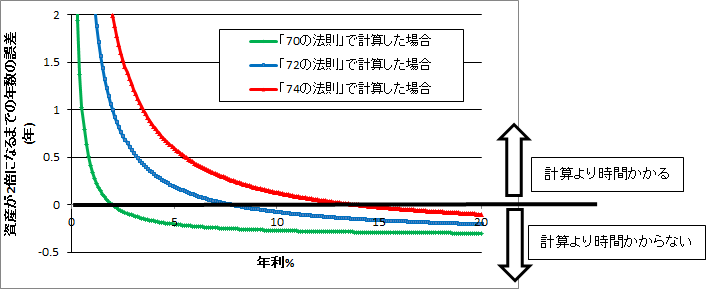
グラフの値が0より大きいと
「〇〇の法則」で計算した年数よりも時間がかかり,
グラフの値が0より小さいと
「〇〇の法則」で計算した年数よりも時間がかからない
ことを表します.
さてここで資産運用の有名どころである
「インデックス投資」の年利リターンを考えます.
ちょっと調べてみますと
日経平均株価:5%くらい
S&P500(米国):10%くらい
参考先
ということがわかりました.
年利がこの範囲に収まる場合の
つまりだいたい年利5~10%くらいの範囲では,
資産が2倍になる年数の差(誤差)を見てみます.
すると
インデックス投資の平均リターンの範囲において,
「72の法則」は他の法則よりも
資産が2倍になる時間(年数)の誤差が小さい
(0に近い)
ということが見て取れるのです.
これが「72の法則」が資産運用において
有名な計算式になった理由だと考えられます.
感想ですが,
シンプルかつかなり合理的な法則だな,と
計算してみて勝手に関心してしまいました.
おわりに
今回投資,資産運用の世界で有名な
「72の法則」について
ホントかいなと思ってしまったので,
指数関数,対数関数の知識で
検証してみました.
誤差はあるものの長期運用を見据えると
「72の法則」合理的な法則であることが確認できました.
我々の生活に関わる資産形成の世界でも
高校数学が関わっていることを
感じていただければ幸いです.
ありがとうございました.
株式投資した得た利益は
場合によっては確定申告で
還付される可能性があります.









コメント