こんな人に読んでもらいたい記事です
・「固有値」,「固有ベクトル」という言葉を聞いたけど,
結局なんの役に立つんだよ
・固有値解析・モード解析って結局なに?
という人
結論
・固有値,固有ベクトルは数学的な説明と,物理的な場面での説明が
うまく結びつきにくい話だと考えています.
→自分も初学者のときはなかなかイメージをつかみにくかったです.
・「行列の固有値,固有ベクトルを求める」とは?
「変換行列(拡大縮小&回転)による一次変換」を
『「定数(固有値)×ベクトル(固有値ベクトル)」の和』で表現すること
・固有値・固有ベクトルがわかると何がうれしい?
①固有値・固有ベクトル行列を使って行列を書き換えることができる
②行列とベクトルで表現された連立方程式(複数の式の関係性を考えないといけない)を
独立した方程式(非錬成)にすることができる
→方程式を解くのが楽になる!
固有ベクトルって何が便利?
こんにちは,りゅういえんじにあです.
固有値,固有ベクトルを初めて習ったとき
「何に使うの?」「何が嬉しいの?」と感じた次第です.
「過去の自分にどう説明するか」という視点で整理してみました.
細かい計算は抜きにして,「行列の固有値,固有ベクトルを求める」と
何が嬉しいのかということに着目して読み物チックに書きます.
細かいことは抜きにして最終的に何ができるの?ということについて
超ざっくり書きますので,詳しいことを知りたい方は線形代数のテキストを
開いてみてください.
「行列の固有値,固有ベクトルを求める」とは,つまり?
そもそも論として行列の固有値,固有ベクトルを求めるとはどういうことか
ざっくり書いておきます.
まず「固有値,固有ベクトルとは?」という話です.
その固有値 \(\lambda_i \ \ \ (i=1,2,3,\cdots,n) \) を持つ
固有ベクトル(列ベクトル) \(v_i\) とすると,
以下が成り立ちます.\begin{align}
A v_i = \lambda_i v_i \tag{1.1} \\
\end{align}
式1.1を読んでみると固有ベクトル\(v_i\)を求めるとは
「変換行列(拡大縮小&回転による一次変換)」を
『「定数(固有値)×ベクトル(固有値ベクトル)」の和』
で表現することです.
もっとざっくり言えば,あるベクトルの表現方法を考えるとき
「拡大縮小+回転で表現していたものを,
あえて新しい座標軸(固有ベクトル)をつかって拡大縮小(固有値)だけで
表現できるようにしたいからそのための材料(固有ベクトル・固有値)を求めてる」
ということになります.
「固有値がわかると何がうれしい?」の一例→方程式を解きやすく!
ある行列の固有値・固有ベクトルの求め方は他に譲り,
無事値が求まったとします.
で,じゃあ何が嬉しいの?という視点で整理しようと思います.
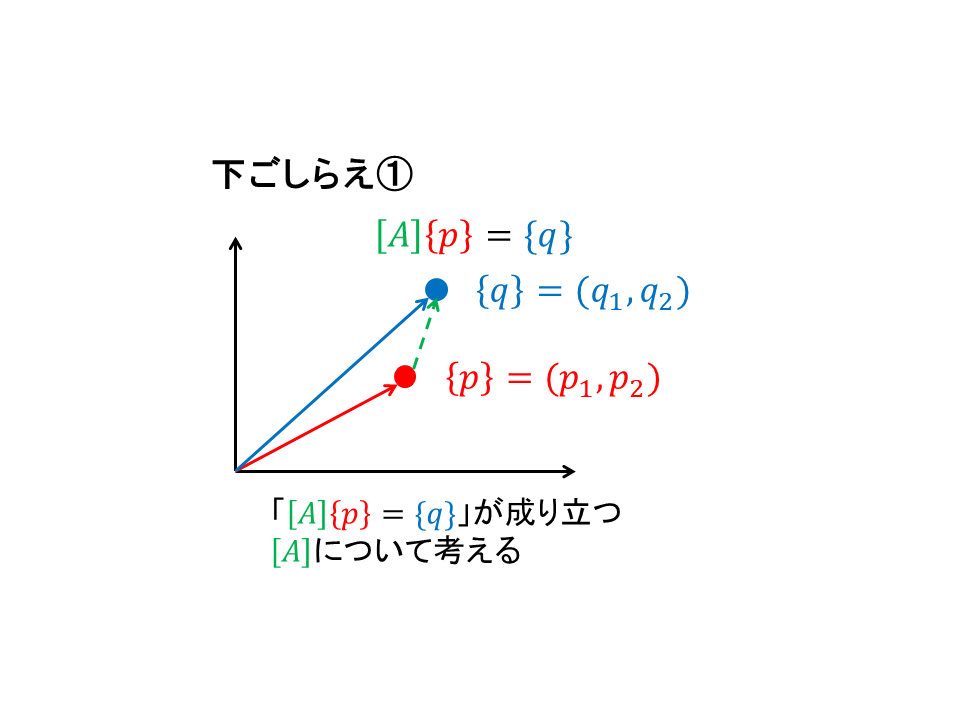
回転行列によるベクトルの変換を考えます.(下ごしらえ①)
高校数学の内容ですが,あるベクトルの回転行列による変換結果は
連立方程式を解くことによって求められます.
連立方程式を考える前に下ごしらえが必要です.
次に固有ベクトルを用意します.(下ごしらえ②)
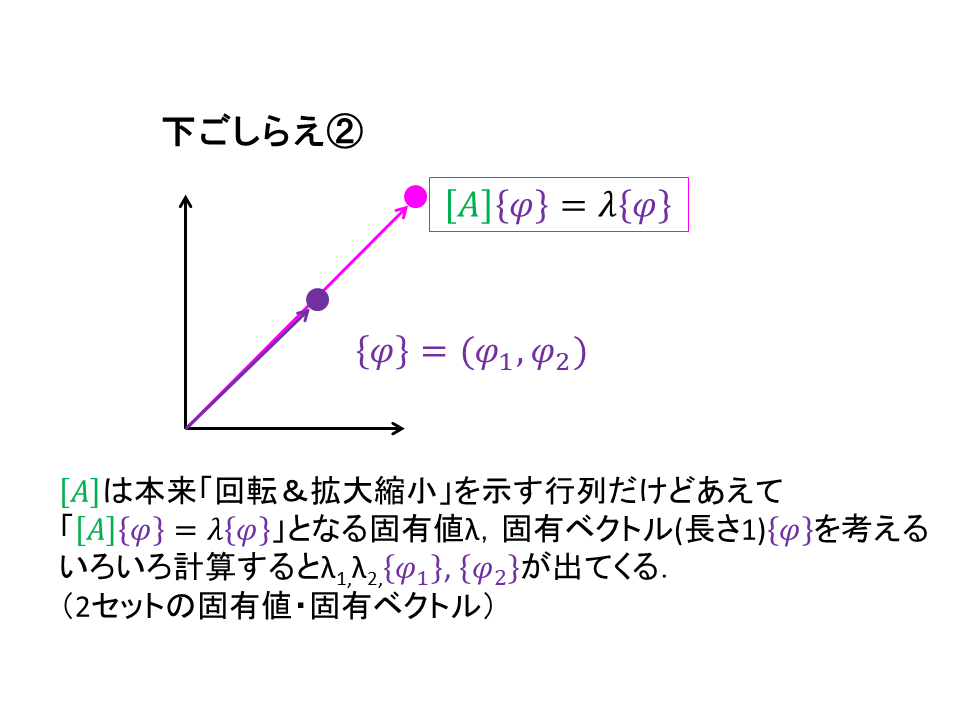
固有ベクトルには直交性があります.
直交性があるということは一次独立つまり
「それぞれの固有ベクトルは他の固有ベクトルとは関係性を持たない,影響されない」
ということを示します.
この固有ベクトルと平行な軸でベクトルを表現することを考えます(下ごしらえ③)
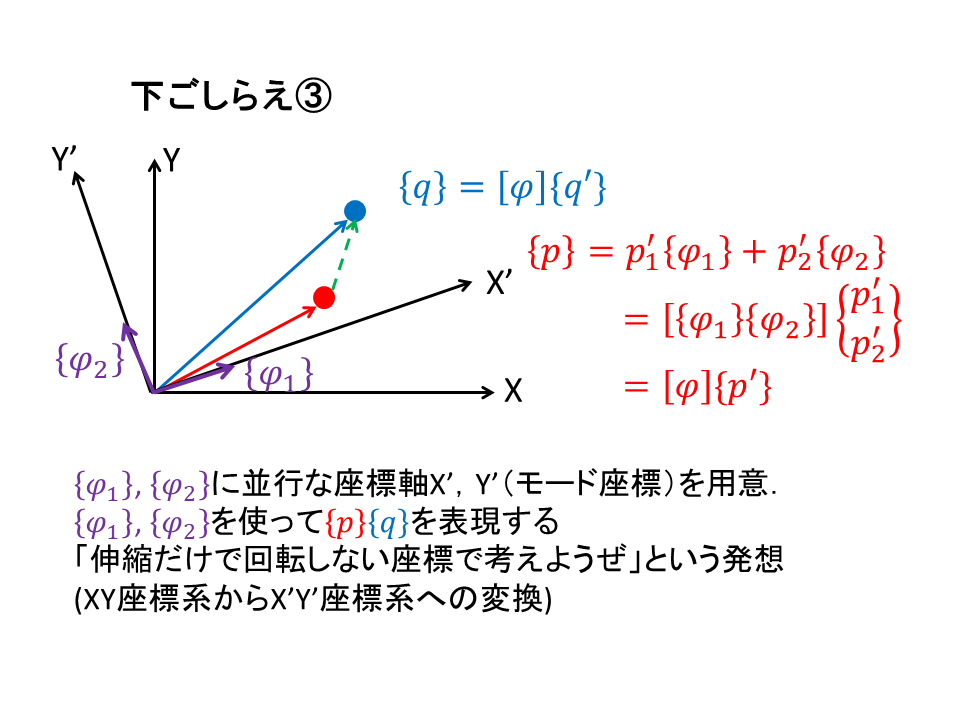
すると固有値,固有ベクトルがわかると,
本来互いに影響しあっていた要素を独立して表現できる,
ようになります.
さてベクトルの回転行列によるベクトル変換を行おうとすると,
先に述べたように要素に分解すると連立方程式を解くことになります.
特徴のない回転行列だと計算がめんどくさいです.
ところが予め固有値,固有ベクトルを使って座標変換を行っておくと,
(表現,基準となる座標軸が違うだけで,同じベクトルを表すため)
対角行列が表れるので,実は連立方程式を解く必要がなくなるのです.
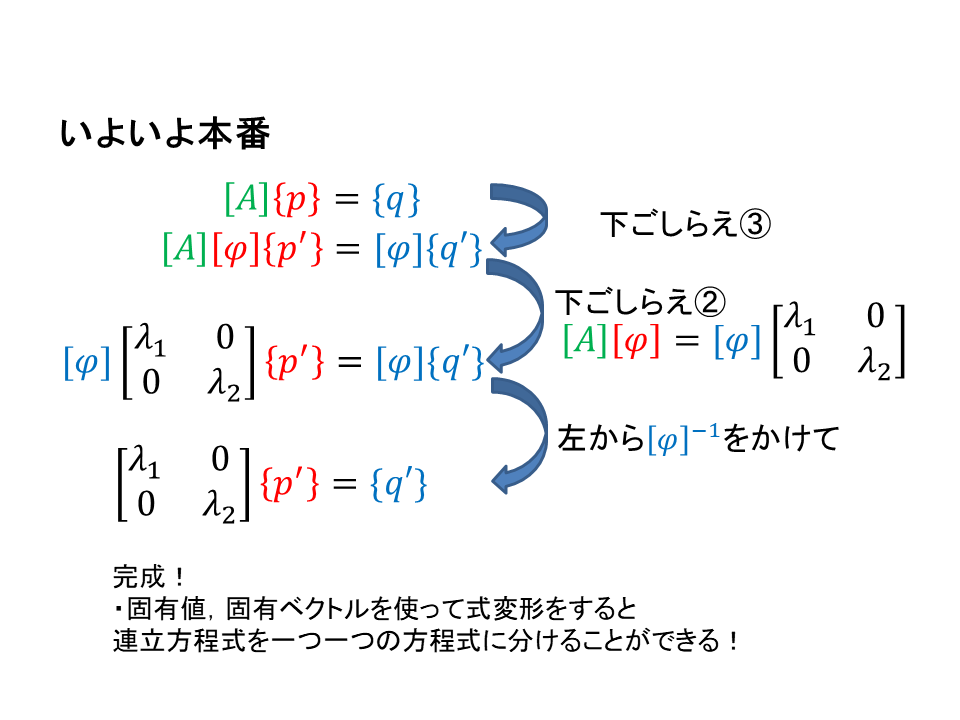
一つ一つの方程式を解くだけでよくなります.
ベクトルのある成分を求めようとしたときに
他の成分の影響(存在)を無視して計算できるようになります.
【実例】機械や建物のモード解析
さて,機械や建物の形状・材質を考えるとき,
「振動モード」というものを考えます.
構造部の振動しやすい周波数,いわゆる共振周波数に応じて「振動モード」が
決まっており,それを考えないと壊れやすい構造部になるなど悪影響があります.
本来影響しあっていた振動を独立して表現するのがモード解析です.
先程,「固有値を求めることで,ベクトルのある成分を求めるときやりやすい」
という話をしましたが,これを利用したものの一つが振動モード解析になります.
構造物は複数の質点,ばね要素が絡んでいるため振動が複雑になります.
ここでいう複雑とは,「お互いの質点の位置関係が他の質点の位置関係に影響する」
モード解析をして書き換えると「モード座標系」になります.
(逆に通常の座標系を「空間座標系」などと言ったりします)
【おまけ】どう勉強するのが良い?
①固有値・固有ベクトルの数学的基礎・計算方法
今回の記事で省略した固有値・固有ベクトルの計算方法は
「線形代数」で扱う分野です.
大学の理工系の学部に進学する,ということであれば基礎教養ということで
必修科目に組み込まれているはずです.
より数学的な側面からゴリゴリ行列,ベクトルの基礎から勉強することになります.
例えばりゅういえんじにあは以下のようなテキストで勉強していました.
マセマのテキストは有名ですね.
②固有値・固有ベクトルの使われ方
固有値や固有ベクトルの使いみちは上記のように,
構造物のモード解析が一つあります.
一方でデータサイエンスの分野で「多変量解析」にも
実は固有値,固有ベクトルが使われています.
実はいろんなところで使われているんですね.
おわりに
今回自分が学生時代に感じていた
「固有値・固有ベクトルってのがあるのはわかったけど,
それがなんの役に立つのよ?」
という疑問に関して,今だったらこう説明するかなという気持ちで
記事を書きました.
ありがとうございました.







