こんな人に読んでもらいたい記事です
・仕事でロータリーエンコーダを使うことになった!
・読み取り装置で1X,2X,4Xってオプションがあるけど,
なんだこりゃ?
・2逓倍,4逓倍は聞いたことあるけど3逓倍とかってないの?
という人
結論
・逓倍:「ていばい」と読みます
→入力パルス数を何倍にするかの設定を表す数,
カウントのルールを決める数のこと
・ロータリエンコーダのパルスのカウント方法を変えると
エンコーダ本体が持つ分解能よりもさらに高い分解能を得ることができる!
2逓倍:エンコーダの分解能の2倍の分解能
4逓倍:エンコーダの分解能の4倍の分解能
制御の基礎的な理屈を交えて勉強すると良いですよ↓
逓倍とはエンコーダの読み方の設定のルール(規則)のこと
こんにちは,りゅういえんじにあです.
モータなどで駆動する軸の回転位置(角度)を計測するのに
ロータリエンコーダ(インクリメンタルエンコーダ)がよく使われます.
『出力される電気信号が「立ち上がり(Low→High)」または「立ち下がり(High→Low)」と切り替わる
回数を数えることで,どれくらい回転したかを知ることができるよ』というものです.
エンコーダの読み取りをする計測器(例えばNI DAQデバイス)では
設定に1X,2X,4Xなどとオプションがあります.
実は1X,2X,4Xなどのオプションは「逓倍」(ていばい)を表すのですが
それらの意味について紹介します.
1X:1逓倍
2X:2逓倍
4X:4逓倍
逓倍(ていばいと読みます)のしくみ
専門的な話は各メーカの情報を参考いただくとして,ざっくりとした理解を目的に記事を書きます.
ザックリ表現すると逓倍とは「入力パルス数を何倍にするか」の設定を表します.
数え方のルールを決めている,と考えるとわかりやすいかもしれません.
まず設定が1(1逓倍)だったときはカウントのルールは
「Low→High(上り)を検出したら1カウントしましょう」です.
この場合一回転あたりのカウント数は変わりません.
例えばエンコーダの1回転当たりのパルス数が1024であったとき,
カウンタ入力値も1024ということになります.
ところがこのカウントの設定(ルール)を変えて
「Low→High(上り)とHigh→Low(下り)をそれぞれで数えましょう」とすると,
2倍カウントするチャンスができるのでカウントされる数を増やすことができるわけです.
上記の例ではエンコーダの1回転当たりのパルス数が1024であったとき,
高速カウンタの入力方法を2逓倍にした場合,エンコーダが1回転すると
カウンタ入力値が2048ということになります.
さらにA相に加えB相(90°の位相差がある)も
カウントすることでさらに2倍のカウントチャンスを得ることができるので
2倍の分解能を得ることができます.
上記の例ではエンコーダの1回転当たりのパルス数が1024であったとき,
高速カウンタの入力方法を4逓倍にした場合,エンコーダが1回転すると
カウンタ入力値が4096ということになります.
同じエンコーダを使っているのに,設定次第で
4倍もの分解能を得ることができるようになるんです.
このようにそれぞれの設定でいつカウントアップされるのかは,
エンコーダの仕様書に付属のタイミングチャートに表現されています.
タイミングチャートとは,以下のように
信号のHighまたはLowの切り替わりが時間ごとに変わる様子を
示した図のことです.
以下にタイミングチャートのイメージ図を示します.
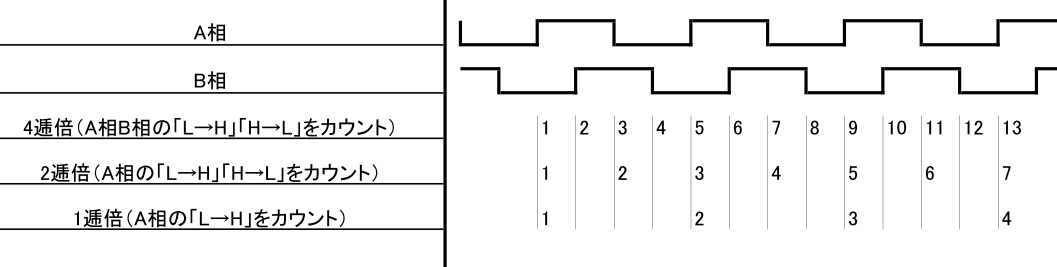
したがっていちいち覚える必要はありません
「こんな考え方があるんだね」くらいでOKです.
あえて整理すると以下のようになります.
(出力がHにいる間のどっかのタイミングでHを検出できればOK),B相不要・2逓倍:A相が「L→H」または「H→L」に切り替わったときだけ1カウントアップ
(出力がHにいる間のどっかのタイミングでHを検出できればOK),B相不要・4逓倍:A相またはB相が「L→H」または「H→L」に切り替わったときだけ1カウントアップ
X逓倍のデメリット ~ノイズに対するバッファがなくなる~
ここまでにX逓倍によってより高い分解能で位置を検出できることを紹介しまいた.
すると
「たった1024の分解能だったのに設定次第で4096になるなんてすごいじゃん」
「じゃあ最初から何も考えずに4逓倍にしてしまえ」
とか考えますよね?りゅういえんじにあもそうでした
でもX逓倍にはデメリットがあるのです.
それは
「ノイズに対して弱くなる,ダブルカウントしやすい」
という点です.
もしくは
「せっかくA相B相の2相でエンコーダを使うメリットを消し去る」
とも表現できます.
「ノイズに対して弱い」ってどういうこと? ~エラーの具体例~
いきなり
「ノイズに対して弱くなる,ダブルカウントしやすい」
と言われてもよくわからないかもしれないので
具体的なエラーの例を順を追って紹介します.
まず大前提を整理します.
大前提その1
エンコーダのカウント数は機械の認識する軸の角度に直結する
→軸の場所(角度)に応じて正しくカウントしたい
大前提その2
電気的なノイズとは信号の瞬間的な
「High→Low→High」または「Low→High→Low」の切り替わりのこと
以上の大前提を頭にいれておいてください.
(1)ノイズ発生!
まず今まで何もなかった(正しくカウントしていた)ところに
電気的なノイズが発生します.
ここでいうノイズとは瞬間的に電圧が上がる(下がる)ことを指します.
原因としては静電気だったりモータのパワーラインに流れる大電流だったり
様々なものが考えられますが,何でも構いません
すると
「エンコーダから出力されている信号はHigh(またはLow)なのに,
瞬間的なノイズでLow(またはHigh)で検出されてしまう」
ことが起こります.
(2)計測器が誤動作する
計測器「信号がHighかLowか」のみでカウントを増やしたり減らしたりするので,
それがノイズかどうかがわかりませんし,関係ありません.
すると
「本当はカウントしてほしくないのに,
カウントされてしまう(角度が進んだように認識されてしまう)」
ということが起こります.
これは結局カウントが勝手に増えてしまうことにつながります.
(3)X逓倍のXが大きくなるほどその影響が大きい
1逓倍(エンコーダのパルス数そのまま)だと,
ノイズでカウントが増えても1カウントで済みます.
しかし,2逓倍だと
「Low→High(上り)とHigh→Low(下り)をそれぞれで数えましょう」
というルールなので一度ノイズが入ると2カウント増える可能性が高まります.
(ノイズの特徴や計測器のサンプリング周期にもよります)
さらに4逓倍だと
「Low→High(上り)とHigh→Low(下り)をそれぞれで数えましょう」が
A相,B相の2つに影響するので,カウント数の誤差が広がる可能性が更に高くなります.
このように,
X逓倍のXが大きくなるほどノイズ影響が大きくなりかねない
ということがデメリットとしてありえるのです.
おわりに
エンコーダのX逓倍の設定について
「過去の自分に説明するならこんな感じ」
ということでまとめてみました.
参考になれば幸いです.
ありがとうございました.






