複素数の使いみちの話～複素数（複素指数関数）で表現すると都合が良いよね，という話～

こんな人に読んでもらいたい記事です

・複素数習ったはいいけど何でそんなもの導入するの？

・複素数の計算自体はできる，知っているけど一体なんの役に立つの？

・複素数は役に立つの？意味あるの？

という人

結論

・複素数の表現の一つ「複素指数関数」を知っておこう

・複素数というより「複素指数関数」が計算ツールとして優秀という話

・微分方程式を解く，ってことを考えると
複素数（複素指数関数）をツールとして使うといろいろ都合が良い

複素数って実際に存在する数じゃないけど…

こんにちはりゅういえんじにあです．

高校の数学のわけのわからない（笑）単元に
「複素数」があります．

計算などは覚えることでできるようになったので，
特に苦手意識を持つことはありませんでした．

とはいえ
「この実際に存在しない数の話が何に役に立つの？」
と思うことが多々残ったままでした

時間が経ち改めて業務で使いそうだったことから
とっちらかっている複素数の話と
微分方程式の話を復習するとなんとなく腑に落ちたので，
備忘録を兼ねてまとめます．

なお当方は工学（エンジニアリング）の視点で
複素数を眺めています．

複素数の表現の一つ「複素指数関数」を知っておこう

後述する通り確かに複素数は便利なツールなんですが，
それは『「複素指数関数」という表現を知っている』
ことが前提だ，ということです．

まず複素指数関数について紹介します．

指数のべき乗の中に複素数zを独立変数としてもつ関数を
「複素指数関数」と言います．

\begin{align}
e^{z}  \tag{1.1} \\
\end{align}

高校数学では複素数zを「実部\(a\)と虚部\(ib\)の和」で表現していましたが，
この複素指数関数を使うと複素数zを
「大きさ（絶対値）Rと偏角\(\theta\)」で
表現できるようになります．
※細かい証明，説明は他に譲ります．

そのときの表現は以下です．

\begin{align}
z &= a + ib   \\
&= Re^{i\theta}  \tag{1.1} \\
\end{align}

そして「実部と虚部の和」の表現と，
「大きさ（絶対値）Rと偏角\(\theta\)」の表現を
つなぐのが有名な「オイラーの公式」です．

\begin{align}
e^{i\theta} &= \cos \theta + i \sin \theta \tag{1.1} \\
\end{align}

「オイラーの公式」について詳しく説明はしませんが，
詳細は検索してみてください．

複素指数関数・オイラーの公式を組み合わせると複素数を
①実数と虚数の和
②大きさと偏角による表現(=大きさと複素指数関数の積)
の二通りで表現できることがわかります．

「大きさと複素指数関数の積」で表現された複素数を使うと
微分方程式を考えるのに都合が良い，ということなのです．

微分方程式を解くことを考えると複素数（複素指数関数）は便利なツールだ

さて高校数学で複素数を扱ったとき
「複素数は様々な計算で使うので，今はその存在・計算方法だけでも知っておいて」
ということを言われはぐらかせれていたのを覚えています．

学校を卒業し仕事を始めて確かに複素数は様々な計算に使うことはわかったのですが，
それよりも
「複素指数関数という複素数表現が画期的だ」
と感じるようになったんです．

例として以下の微分方程式を考えます．

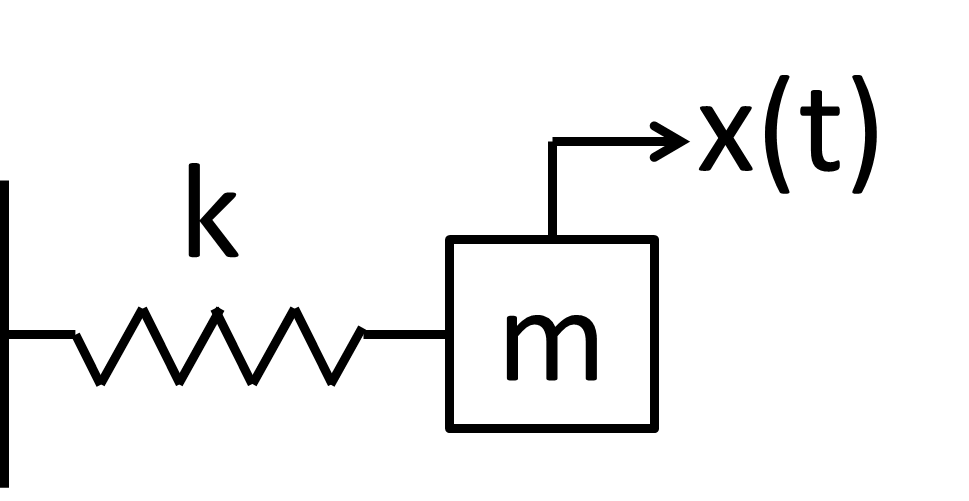
\begin{align}
m\frac{d^2x}{dt^2} +k\frac{dx}{dt} &= 0 \tag{1.1} \\
\end{align}

よくあるバネマス系ですね．
質量mが振動している様子を表現しています．

当然ですがこの運動方程式は振動現象を表しているので，
解は実数になるはずです．

それをあえて「解を複素数で表現する」として
複素指数関数の形で解を仮定すると以下のように都合が良いのです．

(1)二階微分でもとの関数の形になる（複素指数関数）

当たり前ですがそもそも微分方程式は
ある関数とそれを微分した関数の関係を表します．

上記で例として挙げたものは
「元の関数と二階微分した関数の関係を考える方程式」なので，
元の関数と二階微分した関数は同じ（もっと言えば符号が逆）
になっていないといけません．

これを満たすのは
・三角関数
・複素指数関数
のみです．

解としてはどちらの形をとっても良いのですが，
（結局オイラーの公式で変換可能）
複素指数関数を選ぶと都合が良いです．

理由は以下に続く

(2)計算過程，結果がシンプルに表現できる

(1)で解の形は三角関数でも複素指数関数でも表現できそうだ
という話でしたが，なんで複素指数関数を選ぶと都合が良いのでしょうか？

それは計算がシンプル（簡単に）なる，という一点につきます．

まず微分．

高校数学の微分の公式（合成関数の微分）を思い出すと
\(e^{i\theta}\)を\(\theta\)で
一回微分すると\(e^{i\theta}\)に\(i\)を
かけることになります．

\begin{align}
\frac{de^{i\theta}}{d\theta}  &= \frac{de^{i\theta}}{d(i\theta)} \frac{d(i\theta)}{d\theta} &= ie^{i\theta}\tag{1.1} \\
\end{align}

eを底にした複素指数関数を微分すると，
もとの関数に指数にある数をかけた形になります．

簡単ですね．

次に掛け算割り算．

もしこれらの計算を三角関数でやろうとすると，
和積の公式やら合成やら様々な公式を取り出さなくてはならず，
面倒くささ満点になるわけです．

「解は三角関数と複素指数関数どっちの表現でも良いよ」って
言われたら複素指数関数を選ぼうって気になりませんか？

(3)複素数は一つだけで二種類の数を表現できる

上記で述べた通り，複素数は
・実数と虚数の和
・大きさと複素指数関数の積
の二通りで表現できます．

これは
「2つの独立した要素を複素数一個で表すことができる」
ということになります．

例で表した微分方程式の実例においては，
質量mの振動現象（単振動）を表すわけですが，
それを構成する「振幅」や「位相」を複素数一つで表現できるわけです．

この表現に慣れると複素数を見ただけで
「振幅が〇〇で位相は□□」と
判断できるようになり，本や説明書きがシンプルになるということですね．

微分方程式を扱う人の共通言語とも言えるのではないでしょうか？

自分は業務で扱っていたため振動現象からこの活用方法を理解しました．
当時勉強の際参考にした本を示します．↓

 

とはいえ注意点もある（自乗の計算に注意）

このように計算に便利な複素数ですが，
注意点があります．

「複素数zの自乗は大きさRの自乗とは異なる」ということです．
（「実数の自乗は大きさの自乗と等しい」）

まず素直に複素数zの自乗を計算してみます．

\begin{align}
z^2 &= (a + ib)^2   \\
&= (a^2-b^2) + 2iab  \tag{1.1} \\
\end{align}

次に大きさRの自乗を考えます．
複素数の大きさRは複素数平面（実部と虚部の二軸で表現された平面）における
ベクトルの大きさを表しますので

\begin{align}
R^2 &= (a^2 + b^2)  \tag{1.1} \\
\end{align}

つまり以下のようになります．

\begin{align}
z^2 &\neq R^2  \tag{1.1} \\
\end{align}

具体例：エネルギーの計算に注意

ではこれが何に影響するでしょうか？

例えばバネマス系の運動エネルギーを計算するときに影響します．

上記のバネマス系の運動方程式において，
時々刻々と変わるバネの弾性エネルギーを計算することを考えます．

このとき解\(x(t)\)は
①三角関数で表すとき：\(x(t)=A cos(\omega t)\)
②複素指数関数で表すとき：\(x(t)=A e^{i\omega t}\)
とかけます．(A：振幅，\(\omega\)：各振動数)
（詳しい解き方は他に譲ります）

このとき弾性エネルギーUは

\begin{align}
U &= \frac{1}{2} kx^2  \tag{1.1} \\
\end{align}

で表現されます．

同じ方程式の解であるはずなのに①を代入すると正しく，
②を代入するとあやまった値になります．

「本来実数であるはずの解を無理やり複素数（虚数も含めて）で表現している」ためです．

エネルギーを求めるときに単純に複素指数関数で表現された解を
計算に用いると虚数部も計算に入ってしまいます．
ここで「複素数zの自乗は大きさRの自乗とは異なる」が効いてくるわけです．

解は実数であるので，エネルギーは実数部だけ取り出して計算するようにしましょう．

おわりに

今回は微分方程式を考えるにあたって
「複素数（複素指数関数）をツールとして使うといろいろ都合が良い」
ということを紹介しました．

「複素数の計算自体はできる，知っているけど一体なんの役に立つの？」

という人の参考になれば幸いです．

ありがとうございました．