こんな人に読んでもらいたい記事です
・実験でたくさんのデータを扱う
・実験データを解析したらなんかよくわからない結果が出てしまった
・ひとまず手っ取り早く「細かい解析・分析に値するデータか?」を確認したい!
という人
結論
・データを取ったらヒストグラムを作ろう
ヒストグラムを作ることで,計測したデータが解析に値するか真っ先に確認することができます.
実験完了!でもそのデータから意味のある分析ができるかどうか手っ取り早く確認しよう
こんにちは,りゅういえんじにあです.
実験を行ったとき具体的な分析,考察を進めるまえにヒストグラムを作ろうという話です.
分析の前にまず,どんな傾向があるのかを視覚的に確認することができます.
場合によってはそもそもまともなデータとは言えず(現象を正しく計測しているとは言えず),
実験系を直し再度計測する必要があるなど,判断ができます.
ヒストグラムとは計測したデータがどのように分布しているのかを
視覚的に表したものです.
詳しい解説は省略しますが,統計やデータ処理の基本の話なので
書籍をあたるとすぐに出てくる内容です.
統計の基本は以下の書籍などをあたってみるとよいかもしれません.
ヒストグラムでみるデータ収集の結果
ヒストグラムを作ると計測したデータの「正確さ」「精密さ」を視覚的にみることができ,
データが分析するに値するかを確認できます.
「正確さ=真の値と平均の差」で表現でき,どれくらい正しい値(真の値)を計測できるかを表します.
小さいほど「正確に計測できてるね」となりますね
「精密さ=ヒストグラムの広がり」で表現でき,計測値のばらつきがどれくらいかを表します.
小さいほど「偶然やその他の要因で生じる影響が小さい」と判断できますね.
測定器の「精度」と言われているものは上記の正確さと精密さ両方を指します.
(1)正確かつ精密:測定値が真の値を中心として左右ほぼ等しく分布
理想とする計測結果のヒストグラムですね.
平均値と真の値が等しい状態で,真の値からのずれた値は偶然やその他の要因で起こったものとみなすことができます.
以下このヒストグラムとの対比で図を示します.
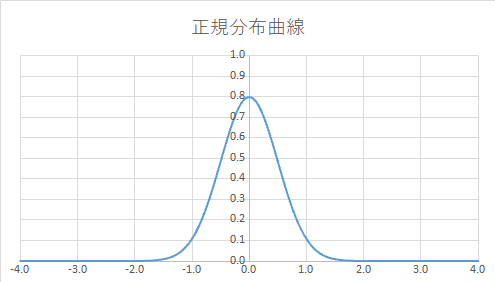
(2)正確であるが精密ではない:(1)に比べてばらつきが大きい
偶然やその他の原因で計測するデータのばらつきσが大きい状態です.
標準偏差σが小さいほど精密さが増し,(1)に近づいていきます.
同じデータ数であればヒストグラムをみると(1)に比べ高さが低くなだらかな山に見えます.
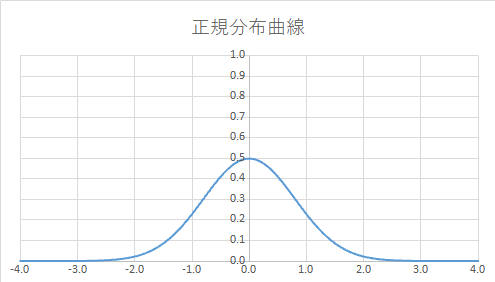
(3)正確ではない(精密さは問わない):測定値の平均が真の値と一致しない
計測されるデータに偏りがみられる状態です.
偏りの原因がわかっている場合はデータ処理で偏りを省いてやることで解決できる場合があります.
「げたを履かせる(履かされている)状態」と口で言ってしまうような状態ですね.
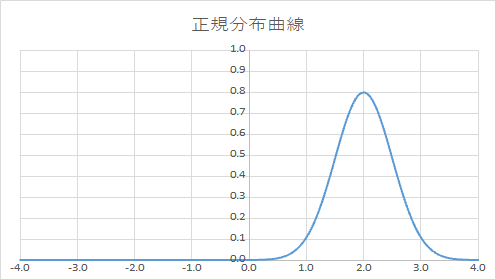
(4)ヒストグラム描いたら正規分布じゃない:測定値として不適切(出直してこい!)
そもそも現象を測定する,ということができていないので「さっさとやり直せ!」と
言われてしまう状態です.
例えばヒストグラムの山が2つ以上出てしまう場合があります.
(仕事の中で何度かやってしまったことがあります)
山が2つあるときは「二峰性」などといいます.
本来複数の性質の現象の集団なのにも関わらず,設定した計測のやり方ではその切り分けができなかった場合に起こります.
本当に見たい現象は何なのか,
その現象「だけ」をダイレクトに計測できる測定の方法は何なのか
など,計測(実験)そのものを見直す必要があります.
他にはデータが山の中に入らず,外れ値として計測されるものもあります.
これは平均値をとる場合影響を受けるので,データの代表を中央値で示すこともありますね.
本格的な測定に入る前に,予備実験的なもので確認をしておきたいものですね.

おわりに
今回データを取ったらヒストグラムを描いて,その計測結果から意味のある分析ができるかを確認しよう,という意図で記事を書きました.
ありがとうございました.






