こんな人に読んでもらいたい記事です.
・感染者数の傾向が気になる人
・「感染者数の減少傾向 全国で鈍化」と言われて,
「これは感染者が増加する前触れに違いない!」と信じて疑わない
・高校数学に指数関数ってのがあるけど,一体どこで役に立つのだろう?
という人
結論
・「感染者数の減少傾向が鈍化」とだけ言われても実態はよくわからない
※指数関数の話を考えれば,感染者数が順調に減少していく過程であっても
減少傾向が鈍化するのはある意味当たり前だから.
・個人的には「感染者数の減少傾向」ではなく
「実効再生産数」の値を気にしようと思います.
※「1」を下回っていれば,時間はかかるかもしれないけど自然と減ってゆく
はじめに
こんにちは,りゅういえんじにあです.
世界中で猛威を奮っている某感染症について
先日(9/24)とあるニュースをみかけました.
新型コロナウイルス対策について厚生労働省に助言する専門家の会合が開かれ、現在の感染状況について、先月下旬以降「全国で感染者数の減少傾向に鈍化が見られる」と評価しました。
この「減少傾向に鈍化が見られる」という文言に
違和感を覚えたのです.
読者のミスリーディングを誘うあまり良くない表現と思います
(メディアとしてはそれを狙っているのかもしれませんが…)
今回はこのことについて,紹介したいと思います.
テレビのコメンテーターの方々も
様々コメントされているかと思いますが,
この情報の捉え方の参考にしていただければと思います.
減少傾向の鈍化?
この記事の感染者数の推移に関する内容をまとめると以下二点です.
(2)「実効再生産数」がより1より小さい値が,だんだん1に近づいている
※実効再生産数:1人の感染者から何人に感染が広がるかを示す指標
この記事では全国的に(2)「『実効再生産数』が1に近づいている」ことから
(1)「減少傾向に鈍化がみられる」と読める表現をしています.
自分は感染症の専門家ではないので
細かいところまでは述べることはできませんが,
はっきり言えることがあります.
それは
(1)と(2)は切り離して考えるべきだ
です.
なぜなら指数関数を考えると
「『実効再生産数』が1に近づいていなくたって
(不変であっても)減少傾向は鈍化する」
からです.
ここを勘違いすると,現状について間違った認識をしてしまうので注意が必要です.
指数関数で考えよう
さて,現在感染者数の推移をみるとき
「実効再生産数」を使ったモデルにて議論がなされています.
上でも述べましたがこれは
「1人の感染者から何人に感染が広がるかを示す指標」
です.
言い方を変えれば
この指標(モデル)にならえば,
「ある人数の感染者から次に何人の感染者が発生するか予想できる」
ということです.
例えば
・「実効再生産数」:0.9
・最初(0回目)の感染者数:100人
とすると
1回目の感染:90人(=100×0.9)
2回目の感染:81人(=90 ×0.9)…
以後続く
となってくものです.
これをグラフに表すと以下のようになります.
(「実効再生産数」は0.9で固定しています)
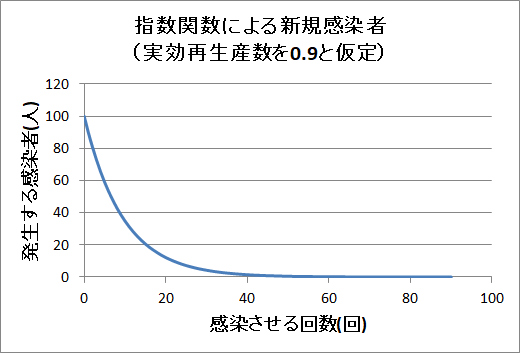
実効再生産数が1より小さいなら減ってゆく
感染の回数を重ねていくうちに新規の感染させる
人数が減っていくことがわかると思います.
(「実効再生産数」は0.9で固定しているにもかかわらずです)
これは高校数学で学ぶ指数関数の話で,以下のような特徴があります.
【指数関数の特徴】
・都度かけられる数(正確には「底」といいます,この例では0.9)が
1より小さければ単調に減少する関数になる.
・ただしその減少の度合いはだんだん小さくなってくる
このように考えると,
単に「感染者数の減少傾向が鈍化」
とだけ言われても実態はよくわからない
言えるのです.
1より大きければ単調に増大する関数になる,
ということになります.
しかもその増え方は「急激」になります.
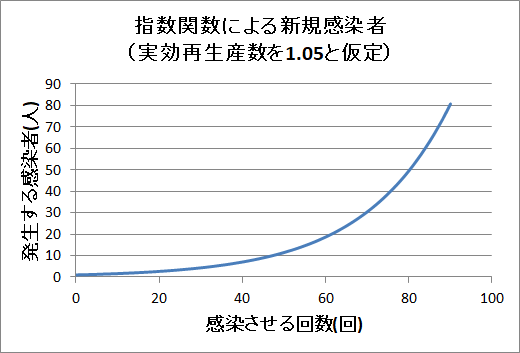
実効再生産数が1より大きいと「急激」に増える…
じゃあどうやって情報をみようか
以上のことを踏まえて,りゅういえんじにあは個人的には
「減少傾向が云々」というよりも
「実効再生産数が1を下回っているか否か」
に注目して日々のニュースを見ています.
「実効再生産数が1を下回っていたら
減っている流れが続いているからよし,
1を超えたら今後増えるかもしれないから注意」
という感じです.
こうすることで感情に振り回されることなく
冷静にいられると思っています.
感情に振り回されず,事実を正しく理解するコツは
以下の本に説明されています.
おわりに
今回は話題の感染症の感染者についてのニュースを,
数字を交えながらどのように読むかを
技術的視点を交えて紹介しました.
こうしたニュースは感情的にとらえてしまいがちですが,
数字を使って考えると冷静に物事をとらえることが
できるようになり,ストレスを軽減できるようになるのではと
思います.
ありがとうございました.
指数関数については
資産形成にも大きな関わりがあります.
詳しくは下記をごらんください.









コメント