こんな人に読んでもらいたい記事です.
・「引張,圧縮,せん断」とかいうけど,
結局どれで荷重受けるのがよいのよ.
・荷重を支える方向どれがいいのかわからない
・日曜大工で作ったものが,
荷重に耐えきれずに壊れた…
・「引張,圧縮,せん断」強度の違いは?
という人
結論
円筒形状の材料で考えます.
(経験的にねじの配置で悩むことが多いため)
・「同じ材料・同じ形状(円筒)」であれば
受けることができる荷重は
「引張圧縮」>「せん断」(>「ねじり」)
の順になります.
・日曜大工で何かを作ろう!
って考えている人にもおすすめ
性質を知って少しでも壊れにくいものを作ろう
結局最適な荷重の受け方ってなんなのよ?
こんにちはりゅういえんじにあです.
機械の分野必須の「材料力学」ですが,
最近意外と忘れていることに気づきました.
学生だったときは
「引張のときはこうだ」とか
「せん断のときはこうだ」とか
説明をされて「なるほどね」と理解したつもりでいました.
でも実際に装置の設計で構造を考えるときに,
「結局どんなふうに荷重を受けるのがいいのよ?」って
話がよくわからなかったんです.
具体的にいうと
「ねじをどの方向から止めればいいの?縦?横?」
「せん断より引張圧縮の方が荷重を受ける方がいいのは
わかるけど,どれくらい差があったんだっけ?」
という話です.
そこで今回は,「同じ材料・同じ形状(円筒)」の材料で荷重を受けるときに
「どんなふうに荷重を受けるようにすれは,許容される荷重が大きくなる?」
という視点で自分の復習を兼ねて整理します.
なお力と言えば運動方程式ですが,
その立式のコツを以下にまとめています.


荷重の方向と荷重(形状:円筒)の整理
材料に荷重Pがかかると内部に応力がはたらきます.
「材料できまる許容応力\(\sigma_max\)に対し
何倍の力がまで耐えられるか」
という視点で整理したいと思います.
(1)引張・圧縮
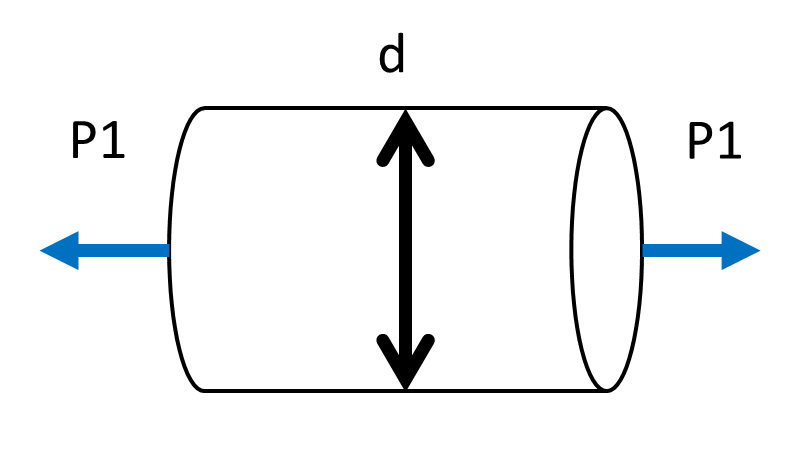
壊れるギリギリの荷重P1と許容最大応力\(\sigma_max\)は
\begin{align}
\sigma_{max}
&= P_1/(\pi(\frac{1}{2}d)^2)\\
&= \frac{4}{\pi d^2}P_1\tag{1.1}\\
\end{align}
(1.1)をP1について整理します.
\begin{align}
P_1
&= \frac{\pi d^2}{4}\sigma_{max}\tag{1.2}\\
\end{align}
(2)せん断
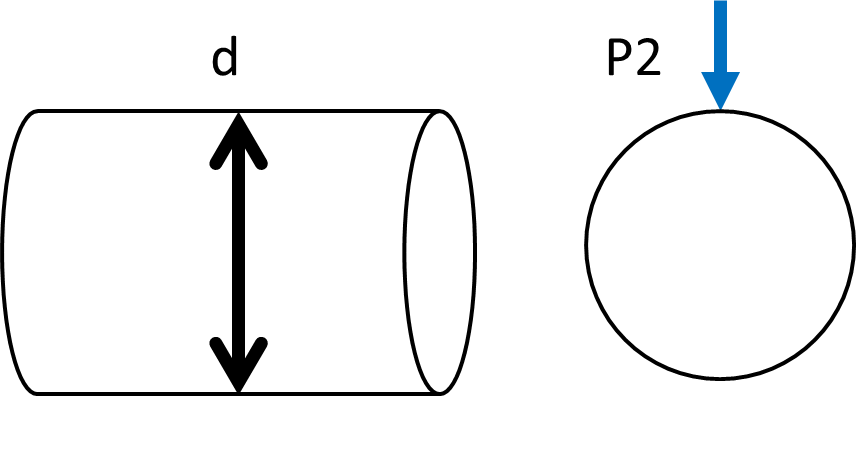
壊れるギリギリの荷重P2と許容最大応力\(\tau_{max}\)は
\begin{align}
\tau_{max}
&= P_2/(\pi(\frac{1}{2}d)^2)\\
&= \frac{4}{\pi d^2}P_2\tag{2.1}\\
\end{align}
同様に(2.1)をP2について整理します.
\begin{align}
P_2
&= \frac{\pi d^2}{4}\tau_{max}\tag{2.2}\\
\end{align}
ここで
「許容せん断応力=許容応力÷√3(≒1.73)」という関係がありますので,
(2.2)をさらに変形します
\begin{align}
P_2
&= \frac{\pi d^2}{4\sqrt{3}}\sigma_{max}\tag{2.2}\\
\end{align}
(3)ねじりによるせん断(おまけ)
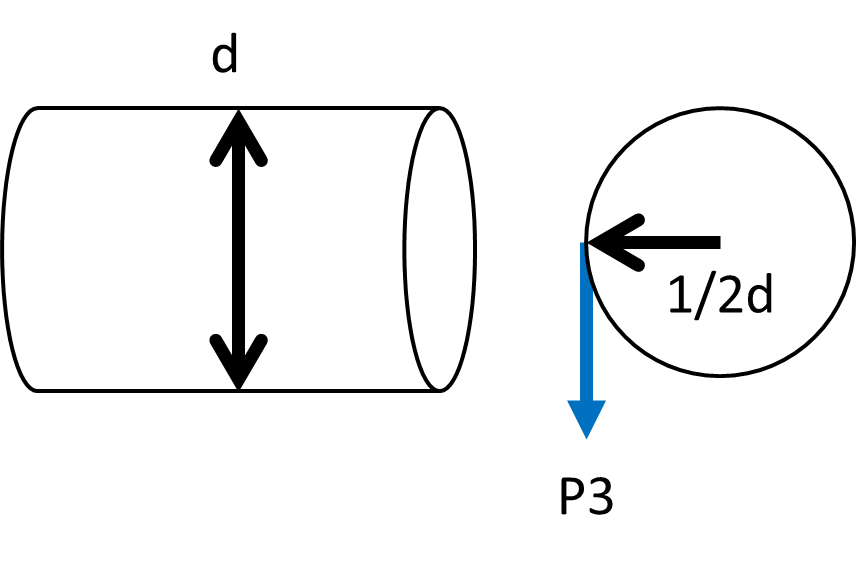
そもそもいきなりねじりで荷重を支えるなんてことは
あまり考えられないのですが,
ねじりのときにどのような形になるのかを整理しておきます.
ねじりは力そのものではなく,トルク(モーメント)で
書きますのでトルクを計算します.
円筒表面からトルクTが発生すると仮定します.
荷重は同じP3とします.
\begin{align}
T
&= P_3\frac{d}{2}\tau_{max}\tag{3.1}\\
\end{align}
円筒のねじりについてせん断応力は以下のように書けます.
\begin{align}
\tau_{max}
&= \frac{16}{\pi d^3}T\\
&= \frac{8}{\pi d^2}P_3\tag{3.2}\\
\end{align}
同様に(3.2)をP3について整理します.
\begin{align}
P_3
&= \frac{\pi d^2}{8}\tau_{max}\\
&= \frac{\pi d^2}{8\sqrt{3}}\sigma_{max}\tag{3.3}\\
\end{align}
(1)~(3)の係数を整理して,
受けることができる荷重は
「引張圧縮」>「せん断」(>「ねじり」)
の順になる.
おわりに
今回機械や構造を作るときに,
「どの向きに荷重を受けさせるのが良いか」という視点で
比較するため情報を整理しました.
同じ材料,形状でも向きによって,
部材が受けることができる荷重が変わるということを
設計や日曜大工に活かしたいですね.
ありがとうございました.








コメント